Perhaps no number is more important to investors than their portfolio’s rate of return. After all, what better way is there to measure your investment performance than to ask:
“What’s my investment portfolio done for me lately?”
Trouble is, it’s usually not so simple to answer this seemingly simple question, and for good reason. There are several ways to calculate your rate of return, and each method has its own strengths, weaknesses, and outcomes.
In this two-part blog series, I’m going to show you two popular ways to calculate your portfolio’s rate of return. In today’s part 1 blog, I’ll cover the time-weighted rate of return (TWRR). In part 2, we’ll take a look at your money-weighted rate of return (MWRR).
By the time we’re through, I’ll have explained how and why each method can produce different results, so you can determine when each one is most appropriate for you.
Understanding the Time-Weighted Rate of Return (TWRR)
When it comes to calculating rates of return, the time-weighted rate of return is your Holy Grail of portfolio performance benchmarking. Because it completely eliminates the effect of cash flowing in or out of the portfolio, it’s the rate of return that mutual funds and ETFs use when preparing their published performance reports.
You calculate the time-weighted rate of return in three broad steps: First, you divide your reporting period into sub-periods – one for each time you made a contribution or withdrawal. Next, you calculate a mini-total return for each sub-period. You then “geometrically link” each of these mini-returns to arrive at the time-weighted rate of return over the entire period.
Let’s see how the time-weighted rate of return works by applying it to three hypothetical investors.
All three of them kicked off 2020 with $100,000 invested in the Vanguard Growth ETF Portfolio (VGRO). Then along came that pesky pandemic, and their portfolios decreased to $77,985 by March 23, 2020.
Now, let’s make some assumptions about each investor’s next steps.
- Investor 1 – We’ll call him “Michael,” doesn’t contribute to or withdraw from his portfolio during 2020. He ends the year with a portfolio value of $110,828.
- Investor 2, “Gob,” adds $10,000 to his portfolio’s VGRO position at the market bottom on March 23. By the end of 2020, his portfolio is worth $125,039.
- Investor 3, “Buster,” panics during the stock market meltdown. On March 23, when his portfolio value has dropped to $77,985, he sells $10,000 out of his VGRO units and withdraws the cash from his portfolio. His portfolio ends the year at $96,616.
Michael’s Time-Weighted Rate of Return
Since Michael didn’t contribute to or withdraw funds from his portfolio during 2020, his time-weighted rate of return is easy to calculate. You simply take his ending portfolio value of $110,828, divide it by the beginning portfolio value of $100,000, and subtract 1. This gives Michael a 2020 return of 10.83%.
However, to accurately compare returns among our three investors, we’ll go ahead and calculate the sub-period returns for all three, including Michael.
I’ll also throw in a spoiler alert: The math I’m about to walk us through is going to reveal that all three investors earned the same, 10.83% time-weighted rate of return.
After any “Scooby moment” you might have about that, you’ll realize this makes sense. All three investors held VGRO – and only VGRO – all year.
So, in this super-simplified example, their time-weighted rates of return will be identical to the 2020 return of VGRO, which was 10.83%.
Now to all that fun math. We’ll start by calculating Michael’s return for sub-period 1 – December 31, 2020 to March 23, 2020. During sub-period 1, his portfolio started at $100,000 and ended at $77,985. Dividing the ending value by the beginning value and subtracting 1 provides us with a sub-period return of -22.01%.
Next, we’ll calculate Michael’s return for sub-period 2, from March 23, 2020 to December 31, 2020. During this second sub-period, the portfolio started at $77,985 and increased to $110,828 by year-end. Dividing the ending value by the beginning value and subtracting 1 gives us a sub-period return of +42.11%.
Finally, we’ll geometrically link Michael’s sub-period returns to obtain his time-weighted rate of return for 2020. To do this, we add 1 back to each sub-period return, multiply the results together, and then subtract 1. Michael ends the year with his time-weighted rate of return of 10.83%.
Gob’s Time-Weighted Rate of Return
As mentioned earlier, Gob also started the year with $100,000 invested in VGRO, and his holdings had also dropped to $77,985 by March 23. But then, Gob added $10,000 to his VGRO position, increasing his portfolio value to $87,985. By the end of 2020, his portfolio had grown to $125,039.
Following the same steps, we start by calculating Gob’s sub-period 1 return from January 1, 2020 to March 23, 2020. Just as with Michael’s identical portfolio, his sub-period 1 return was the same -22.01%.
We then calculate Gob’s sub-period 2 return from March 23, 2020 to December 31, 2020. For the start date, we’ll use the portfolio value after the cash flow occurred. During this second sub-period, the portfolio started at $87,985 – or $77,985 plus his $10,000 contribution. It increased to $125,039 by the end of the year. Dividing the ending value by the beginning value and subtracting 1 gives us a sub-period return of +42.11%.
Geometrically linking Gob’s two sub-period returns again yields a time-weighted rate of return of 10.83% for the year.
See what I mean about those identical returns for identical holdings during identical holding periods?
Buster’s Time-Weighted Rate of Return
But to really drive home the point, let’s calculate Buster’s time-weighted rate of return. He also started with $100,000 invested in VGRO at the beginning of 2020. And on March 23, 2020, his portfolio was also worth $77,985. On that date, he withdrew $10,000, bringing his portfolio value down to $67,985. By the end of 2020, his portfolio value stood at $96,616.
Using the same calculations as before, Buster’s sub-period 1 delivered a return of (you guessed it) -22.01%. During sub-period 2, when his portfolio started at $67,985 and increased to $96,616, Buster’s time-weighted rate of return was, again, +42.11%. Finally, geometrically linking the two sub-period returns provides us with a time-weighted rate of return for the year of 10.83%.
Again, this identical 10.83% annual return for all three of our intrepid investors is precisely the result we should expect.
The way we calculate the time-weighted rate of return is supposed to wipe out the effect of individual contributions and withdrawals, revealing the annual return that VGRO delivered to all three investors who held the fund throughout 2020.
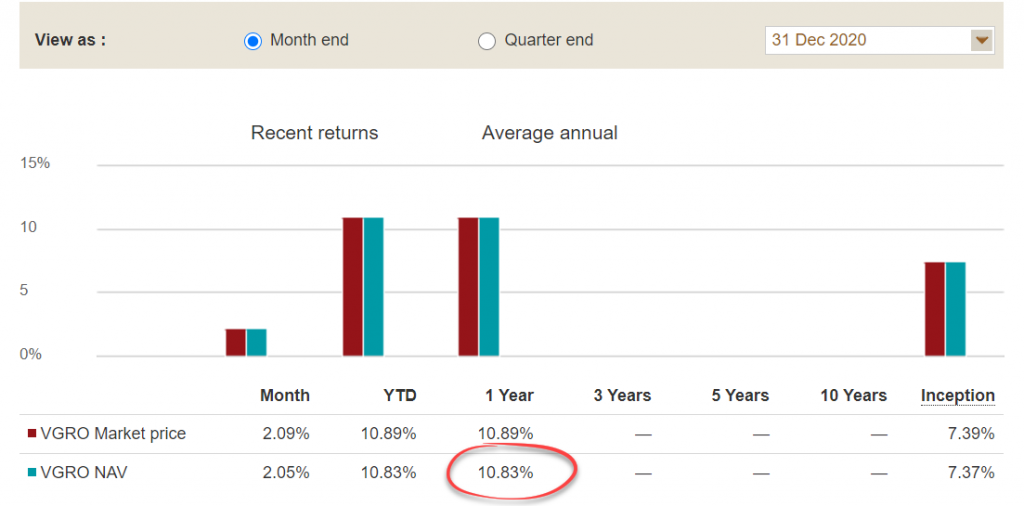 Source: Vanguard Investments Canada Inc. as of December 31, 2020
Source: Vanguard Investments Canada Inc. as of December 31, 2020
If you’re catching my drift, this makes the time-weighted rate of return ideal for benchmarking different portfolio and fund managers. It’s especially good at comparing various active managers’ investment strategies.
Unfortunately, while the time-weighted rate of return is useful for mutual funds and portfolio managers, it’s impractical to deploy for your own, DIY portfolio. First, there’s all that math. Plus, even if you had an easy way to crunch all those numbers, the data is hard to come by to begin with. You’d need to know your total portfolio value on any day you contributed to or withdrew cash from your portfolio. Your discount broker typically doesn’t report these values in your account statements.
Which brings us to another popular way to wrap your head around your returns … your money-weighted rate of return (coming up next!).